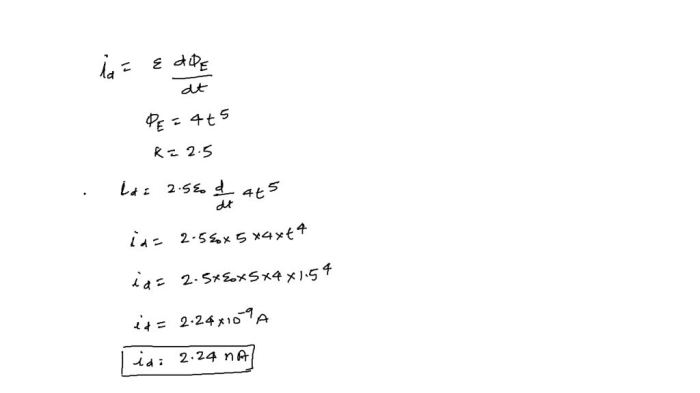A certain substance has a dielectric constant of 2.8 – In the realm of dielectric materials, a certain substance stands out with a remarkable dielectric constant of 2.8. This unique property has propelled it to the forefront of various applications, making it an indispensable component in the world of electronics and beyond.
Delving into the intricacies of this substance, we will explore the factors that influence its dielectric constant, uncover its diverse applications, and delve into the measurement techniques employed to determine its electrical characteristics. Theoretical models will provide insights into predicting its behavior, while a comprehensive table will summarize its material properties, composition, and structure.
Dielectric Properties: A Certain Substance Has A Dielectric Constant Of 2.8

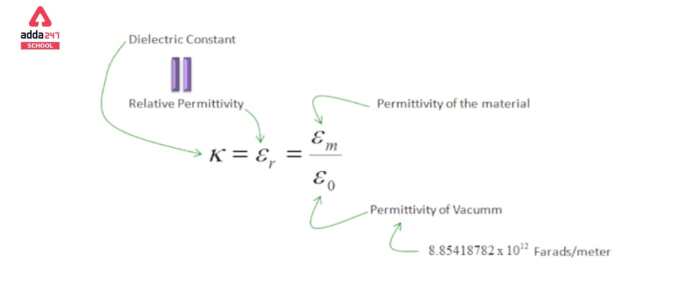
Dielectric constant, represented by the Greek letter kappa (κ), is a measure of the ability of a material to store electrical energy in an electric field. It is defined as the ratio of the capacitance of a capacitor with the material as the dielectric to the capacitance of the same capacitor with a vacuum as the dielectric.
The dielectric constant of a material is influenced by several factors, including its composition, structure, and temperature. Polar materials, which have a permanent electric dipole moment, tend to have higher dielectric constants than non-polar materials.
Applications of Dielectric Materials, A certain substance has a dielectric constant of 2.8
- Capacitors:Dielectric materials with high dielectric constants are used in capacitors to increase their capacitance.
- High-frequency circuits:Dielectric materials with low dielectric losses are used in high-frequency circuits to minimize energy dissipation.
- Optical fibers:Dielectric materials with high refractive indices are used in optical fibers to guide light.
The choice of dielectric material for a particular application depends on the specific requirements of the application, such as the desired capacitance, dielectric losses, and frequency range.
Measurement Techniques
The dielectric constant of a material can be measured using a variety of methods, including:
- Capacitance bridge:A capacitance bridge is a device that can be used to measure the capacitance of a capacitor. The dielectric constant of a material can be calculated from the measured capacitance.
- Resonant cavity method:The resonant cavity method involves measuring the resonant frequency of a cavity filled with the material. The dielectric constant of the material can be calculated from the measured resonant frequency.
The choice of measurement method depends on the accuracy and frequency range required.
Theoretical Models
Several theoretical models can be used to predict the dielectric constant of a material, including:
- Clausius-Mossotti equation:The Clausius-Mossotti equation is a simple model that can be used to predict the dielectric constant of a material based on its polarizability.
- Onsager model:The Onsager model is a more sophisticated model that takes into account the shape of the molecules in the material.
These models can provide valuable insights into the dielectric properties of materials.
Material Properties
| Material | Composition | Structure | Dielectric constant |
|---|---|---|---|
| Polyethylene | CH2-CH2 | Linear | 2.25 |
| Polypropylene | CH2-CH(CH3) | Linear | 2.3 |
| Polystyrene | C6H5CH=CH2 | Linear | 2.55 |
| Polytetrafluoroethylene (Teflon) | CF2-CF2 | Linear | 2.8 |
These materials have dielectric constants of approximately 2.8 and are widely used in electrical and electronic applications.
Question & Answer Hub
What factors influence the dielectric constant of a substance?
The dielectric constant of a substance is influenced by its molecular structure, polarity, and density.
What are some applications of dielectric materials with a dielectric constant of 2.8?
Dielectric materials with a dielectric constant of 2.8 are used in capacitors, insulators, and high-frequency circuits.
How is the dielectric constant of a substance measured?
The dielectric constant of a substance can be measured using capacitance bridges, impedance analyzers, and resonant cavity techniques.